Tutorial 2 - Understanding fMRI Statistics and Statistical Maps
Goals
To understand how statistics, even simple statistics such as correlations, can be employed on a voxelwise basis to analyze fMRI data
To understand the significance of correlation coefficients and p values in time course analyses
To understand how to interpret simple statistical maps
Relevant Lectures
Lecture 03a: fMRI statistics: Correlation
Lecture 03b: fMRI statistics: Using the General Linear Model (GLM) to do a correlation
Accompanying Data
Background and Overview
This lecture assumes that you have an understanding of basic statistics. If you have taken a stats course in Psychology and worked with behavioral data, many of the statistical tests that can be employed for fMRI will be familiar to you — correlations, t tests, analyses of variance (ANOVAs) and so forth. These tests can be applied to fMRI data as well, using similar logic. This tutorial will introduce correlation as a way of testing the reliability of brain signal. More specifically, we will use correlation to test the degree of association between an expected time course (predictor) and the actual time course (signal) from a voxel (or a cluster of voxels in a specific brain region).
Understanding fMRI statistics for data over time
Any statistical test needs two pieces of information:
- signal: how much variance in the data can be explained by a model (e.g., a correlation, a difference between two conditions in a t test, or a difference between a combination of conditions in a factorial design that is analyzed by an ANOVA)
- noise: how much variance remains unexplained
Statistical significance -- the degree of confidence that an effect is "real" depends on the ratio of explained variance to total variance (explained + unexplained variance). Put simply, if you have a big difference between conditions and little variance within each condition, you can be quite confident there is a legitimate difference; whereas, if you have a small effect in a very noisy data set, you would have little confidence that there was really a difference.
For fMRI data, there are two levels at which we can compute variance.
- Variability over time. If we only have data from one participant, we can look at how the strength of a difference in activation relative to the variability of the time course in a given voxel or region. This temporal variability can be parsed into effects due to the expected changes between conditions vs. noise. In this case, data points are time points.
- Variability over participants. If we have data from multiple participants, we can look at the average size of an activation difference across participants relative to the variability among participants. In this case, data points are participants.
In this tutorial, we will examine the first case -- how statistics can be used in the data from a single participant to estimate effect sizes relative to variability over time. We will begin with a Pearson correlation, which is one of the simplest and most straightforward statistical tests to understand. In later tutorials (Tutorial 4 and 8), we will learn how to employ the second approach, in which we can combine data between participants and look at the consistency of effects across individuals.
Time Series: Data, Signal, and Noise
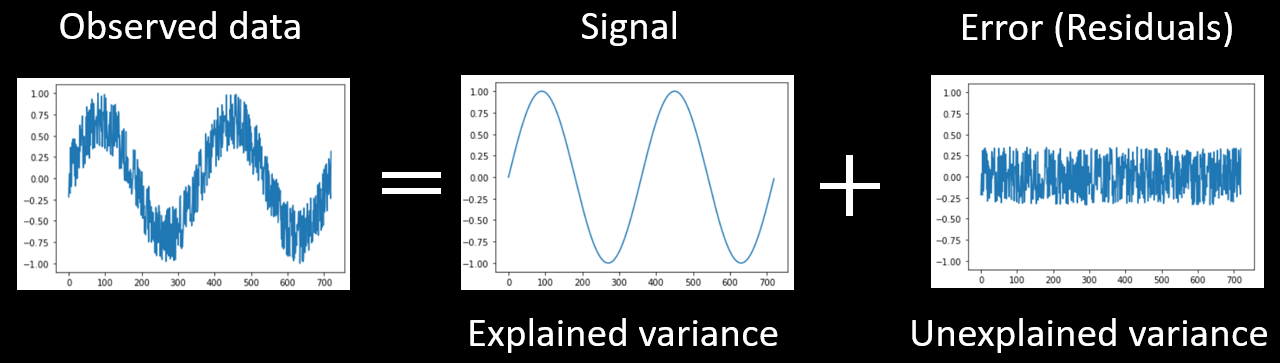
Let's begin by looking at how we can statistically analyze data that changes over time. A time course is shown below. This time course depict fMRI activation over time... or it could be any kind of time series (e.g., daily temperature over a two-year period).
We might be able to explain some of this variability with a model that captures much of the variability in the data, here a sinusoidal model of changes over time. The variance that can be accounted for by the model is the signal. However, the model can not explain all of the data. The error or noise (the part of the variance we cannot explain/model) can be seen in the residuals, which are computed by subtracting the model from the data.
These three parts are depicted in Figure 1 below.
Figure 2-1. Any data (such as a time series) can be decomposed into explained and unexplained variance.
Applying correlations to time-series data
In order to determine whether a voxel is reliably reacts to a certain stimulus, we must first measure how reliabily it changes with that stimulus/condition. To do this, we can use correlations to asses how closely the pattern of a predictor is related to the time course. A high correlation between a predictor and a timecourse indicates that the voxel's or region's activity is highly related to the type of stimuli presented, while a low correlation indicates that the voxel's or region's activity is not related to that specific type of stimuli.
Another way of thinking about it is in terms of signal-to-noise ratio . One way of quantifying this is calculating the percent of explained variance (explained variance/total variance). This perentage can easily be calculated by squaring the correlation coefficient(r2). A high signal to noise ratio(lots of signal with little noise) will have greater percent of explained variance, while a lower signal to noise ratio (little signal with lots of noise) will result in a smaller percent of explained variance.
Let's examine a few simple cases.
Activity #1
Open Widget 1 in a new window by clicking on the plot. (Note: if you have trouble opening the animation, please see our troubleshooting page).
Widget 1 shows a simulated 'data' time course in grey and a single predictor in purple using arbitrary units (y axis) over time in seconds (x axis). The predictor can be multiplied by a beta weight (scaling factor) and a constant can be added using the sliders (more will be said on these two parameters later in the tutorial). Below the time course is the residual time course, which we obtain by subtracting the model -- that is the scaled predictor -- from our data at each point in time (i.e., data - predictor = residuals).
Adjust the sliders for Voxel 1 so that the purple line (predictor) overlaps the black line (signal). Once you are done, click on the Optimize GLM button. This will give you the optimal beta/slider estimate.
Question 1:
a) What is the value of the correlation coefficient?
b) What does this value mean?
- It is a strong positive correlation between the predictor and the signal.
- It is a weak positive correlation between the predictor and the signal.
- It is a perfect correlation between the predictor and the signal.
- There is no correlation between the predictor and the signal.
c) What percentage of the total variance would the best model account for? What percentage of the total variance does the current model (purple predictor) explain? Is this the best model possible? Why or why not?
In practice, we don't expect to find a perfect fit between predictors and data. Voxel 2 is a more realistic example of noisy data.
Select Voxel 2 and adjust the sliders until you find the beta weight and constant that best fit the data.
Question 2:
a) What is the new correlation coefficient? Why is it different from Voxel 1?
b) What percentage of the total variance does the current model(purple predictor) explain for Voxel 2? What can we say about the difference in signal to noise ratio between Voxel 1 and Voxel 2?
c) How is the top scatter plot for Voxel 1 different from the scatter plot for Voxel 2? How does this difference relate to the correlation coefficient?
d) Do the correlation coefficient and beta weight quantify the same thing?
- Yes, both quantify the strength of a relationship.
- No, correlations quantify the strength of activation and beta weights quantify the strength of the relationship.
- Yes, both quantify the strength of the activation.
- No, correlations quantify the strength of relationship and beta weights quantify the strength of the sctivation.
Applying correlations to real fMRI data
Now let's look at some real time courses by considering the simplest possible example: one run from one participant with two conditions. Note that we always need at least two conditions so that we can examine differences between conditions using subtraction logic. This is because measures of the BOLD signal in a single condition are affected not only by neural activation levels but also by extraneous physical factors (e.g., the coil sensitivity profile) and biological factors (e.g., the vascularization of an area). As such, we always need to compare conditions to look at neural activation (indirectly) while subtracting out other factors.
In this case, we will look at the first localizer run. Recall that this run is composed of four visual conditions (faces, hands, bodies and scrambled) and 1 baseline condition. For now, we will group the four visual conditions into one visual condition, leaving us with only two conditions (visual stimulation vs baseline).
Activity #2
Open the widget in a new window and adjust the sliders to fit the visual predictor (in pink) to Voxel A's time course as closely as possible.
Question 3:
a) How many data points are there in total? How many degrees of freedom (df) does the model require? Conceptually, what does this/do these df correspond to? How many df are assigned to the residuals?
b) What is the correlation coefficient for Voxel A? How would you interpret this coefficient in terms of strength of the relationship and the voxel's response to visual stimulation? What is the percentage of explained variance?
c) How much variance does the model account for Voxels A, B, C and D. What is the most obvious factor that hinders the fit of the model for Voxel B?
The model accounts for ____, ____, ____ and ____ of the total variance for voxels A, B, C and D respectively. ____ greatly hinders of the fit of the model for Voxel B.
d) Voxel D has a correlation of r = -0.38. How do you interpret a negative correlation for fMRI data?
- The signal is below the baseline when the stimuli are presented.
- The signal is slightly above the baseline when the stimuli are presented.
- The signal doesn’t change from the baseline when the stimuli are presented.
- There is no signal, it’s all noise.
e) Voxels E and F have interpretable time courses but the correlations are not very high. Why?
What about p values?
There is always a chance that a certain pattern of data could occur randomly. For example, if you flip a normal coin 10X in a row, there is a small but non-zero chance -- p = 0.510 = .001 = 1/1000 = 0.1% -- that heads could occur on every flip. If we were trying to determine whether a coin was a magical "heads-only coin", getting 10 sequential heads outcomes would lead us to be fairly confident that it was. Of course, we would be less confident if we only got three heads outcomes, in which case the likelihood due to chance would be p = 0.53 = .125 = 1/8 = 12.5%. And we would be more confident if we got 20 sequential heads outcomes, in which case the likelihood due to chance would be p = 0.510 = .000001 = 1/1,000,000. Thus as you can see, one factor that reduces the likelihood of chance findings is the amount of data acquired. Generally researchers are willing to believe any outcome that has a likelihood of arising due to chance of p < .05 = 5%. Such results are deemed statistically significant.
The p value is the probability of obtaining a given result purely due to chance, as estimated based on how noisy the data are. Because the correlation estimates how much of the variability in the data is explained, higher r values will be associated with lower p values.
Question 4:
a) Using your answers from Question 3 above along with the "p from r" section of this online statistical calculator, determine whether or not the correlations for Voxels A, B, C and D are statistically significant (when no correction for multiple comparisons is applied).
b) Is a p value always associated to the same correlation coefficient? Why or why not?
c) If we use a threshold of p < .05 and examine the correlation between a predictor and a time course for 100 different voxels (basically, we calculated 100 correlations), how many voxels might be statistically significant due to chance? If we used a threshold of p < .01? What type of error (I or II) increases with the number of statistical tests?
Modelling the hemodynamic response
Recall that fMRI is an indirect mesure of neural activity. The expected neural activation is often modeled using a box car function. We then use a mathematical procedure called convolution to model the expected BOLD response based on the known relationship between neuronal activity and BOLD -- the hemodynamic response function (HRF) .
Let's first understand why having an accurate model of BOLD, based on the HRF, is valuable.
Using Widget 3, find the best parameters for the neural (box car) model and note the correlation and error term (squared error).
Then press on the convolve button to transform the boxcar function into the HRF. Again find the best parameters for the BOLD (convolved) model and note the correlation and error term (squared error).
Question 5:
a) Based on shape of the BOLD predictor, which type of Hemodynamic Response Function was employed in the convolution?
- Two-gamma function
- Gamma function
- Box-car function
- Boynton function
- Square-wave function
b) How does the convolution affect the quality of the model fit? What would be the consequences of using an HRF that did not match the participant's actual hemodynamics well (for example, if you used the standard model on a participant who had a much larger post-stimulus undershoot than most)?
II. Whole-brain Voxelwise Correlations in BrainVoyager
In the previous sections, we learned how to quantify the strength of the relationship between a predictor and a time course for a single voxel using correlation coefficients and p-values. However, we have 194,000 resampled functional voxels inside the brain volume. How can we get the bigger picture?
One way is to do a "Voxelwise" analysis, meaning that we run not just one correlation but one correlation for every voxel. This is sometimes also called a "whole-brain" analysis because typically the scanned volume encompasses the entire brain (although this is not necessarily the case, for example if a researcher scanned only part of the brain at high spatial resolution).
Instructions
1) Load the anatomical volume and the functional data. This procedure is explained in tutorial 1, but will be reminded for you here:
- Anatomical data: Select File/Open... , navigate to the BrainVoyager Data folder(or where ever the files are located), and then select and open sub-10_ses-01_T1w_BRAIN_IIHC.vmr
- Functional data: Select Analysis/Link Volume Time Course (VTC) File... . In the window that opens, click Browse , and then select and open sub-10_ses-01_task-Localizer_run-01_bold_256_sinc3_2x1.0_NATIVEBOX.vtc , and then click OK . The VTC should already be linked to the protocol file. You can verify this by looking at the VTC properties (follow steps in Tutorial 1).
Now we can conduct our voxel-wise correlation analysis.
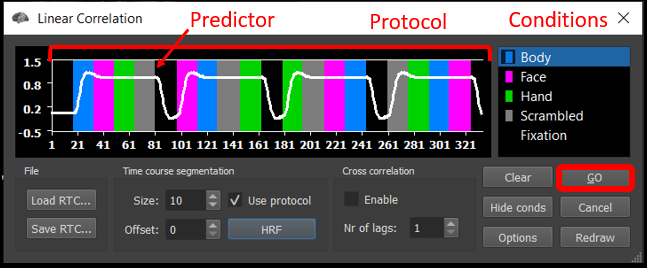
Figure 2-2. Menu to compute Linear Correlation Maps
2) Select Analysis/Compute Linear Correlation Maps...
Now let's generate a box car function with the expected neural response (high for the four main conditions, low for the baseline). If you are using a PC, left-click on any black period and right-click on the blue, pink or purple/green and gray periods. If you are using a Mac, click on any black period and control-click on some part of each of the four colored periods.
Once you have the expected box car function, click on the HRF button to convolve the predictor with the default exercise.
Optional: If you want to see the effect of using a different HRF, you can clear the predictor, regenerate the box car predictor, go into options, select the HRF tab, select Boynton, click OK, and then click HRF. After this, however, repeat these steps using the default two-gamma function.
Click GO.
Figure 2-3. Explanation of how to manually create a box car predictor and convolve it.
Figure 2-4. Shows how the convolved predictor should appear.
Running a voxelwise correlation computes one statistical parameter for every resampled functional voxel (here 194,000 r values). Since we did a correlation, the parameter is r, but as we will see later, other parameters can be estimated (e.g., t for a paired samples contrast, F for an analysis of variance, ANOVA).
Parameters be visualized by generating a statistical "heat map" in which each voxel is assigned a color based on the value of the statistical parameter. (Now you understand what a statistical parametric map is and why a classic fMRI analysis software package is called SPM).
The heat map is generated by assigning a color to each voxel (or leaving it transparent) based upon the level of the parameter. This correspondence is determined by a look-up table (LUT).
Maps are typically overlaid on the anatomical scan to make it easier to see the anatomical location of activation (but remember the map was generated from the functional scans).
If you hover your mouse over different voxels, you will see the correlation coefficent(r) and p value for any given voxel.
Toggle between two different look-up tables that BrainVoyager provides. Select File/Settings..., and in the GUI tab, try out two default options: "New Map Default Colors (v21+)" an "Classic Map Colors (pre-v21)" and click Apply after each selection.
Note: The course slides and tutorials use the Classic colors.
Figure 2-5. Activation depicted with BrainVoyager’s Classic LUT
Figure 2-6. Hovering the mouse over a voxel will show its coordinates, intensity, statistical parameter value and p value.
The mapping between parameter values and the colors in the look-up table (on the right side of the coronal view) can be adjusted. The most important setting is the minimum value or the threshold. Any correlation coefficients closer to zero than the minimum do not get mapped to a color (i.e., the voxels are rendered as transparent). For example, if the threshold is r = .3, they only voxels with r > .3 or r < -.3 will be colored.
There are a few ways to modify the threshold.
3) First, you can adjust the threshold by using the icons (circled in red) in the left side bar. Try it.
Alternatively, if you want to employ a specific threshold, there is a more precise way.
Figure 2-7. The minimum p value (threshold) can be quickly adjusted using these buttons to increase the threshold (bigger blob button) or decrease the threshold (smaller blob button).
4) Select Analysis/Overlay Volume maps... . This will open the Volume Maps window. Next, click on the Statistics tab. Here, we can set the maximum and minimum correlation threshold manually in the Correlation range section. Try changing the min and max values and observe the result on the statistical maps.
Question 6:
a) Look at the color scale on the right of the coronal view. What do the numbers on the scale represent? What do the warm and cool colors represent?
b)How do the numbers on the scale change when decreasing and increasing the threshold? What do the warm and cool colors represent?
c) Set the threshold to zero and explain what you see. Why are there colored voxels outside the brain? What could we do to limit the colored voxels to the brain volume?
d) Set the minimum threshold to 0.30 and the maximum threshold to 0.80. What occurs when you increase the minimum threshold while keeping the maximum threshold constant? If you keep increasing the minimum threshold, how does your risk of Type I and Type II statistical errors change?
e) Where would you expect significant activation for this contrast? Where would you NOT expect to see legitimate activation for this contrast? Bonus Question: There is one region where you wouldn't expect legitimate activation but you still see very strong activation even with moderately high thresholds. Do you have any idea what might cause this?
f) What effect does decreasing and increasing the maximum have? What is a good strategy for choosing the maximum value?
Figure 2-9. A specific p value can be specified in Map Options tab of the Volume Maps panel.
5) Now, click on the Map Options tab. Here, we can set a threshold using p values instead of correlation coefficients.
Question 7: Set the threshold to p < .05 and click Apply. Given that a p-value threshold of .05 is the usual statistical standard, why is it suboptimal for voxelwise fMRI analyses?
In the next tutorial, we will consider strategies to deal with this problem.